【視聴数 54560】
【チャンネル名 数学を数楽に】
【タグ 動画,ビデオ,共有,カメラ付き携帯電話,動画機能付き携帯電話,無料,アップロード,チャンネル,コミュニティ,YouTube,ユーチューブ】
FX/暗号資産の投資動画リンクまとめ FX・暗号資産のyoutube動画をまとめました!最新のFX・暗号資産投資情報や役立つFX・暗号資産投資情報があります!
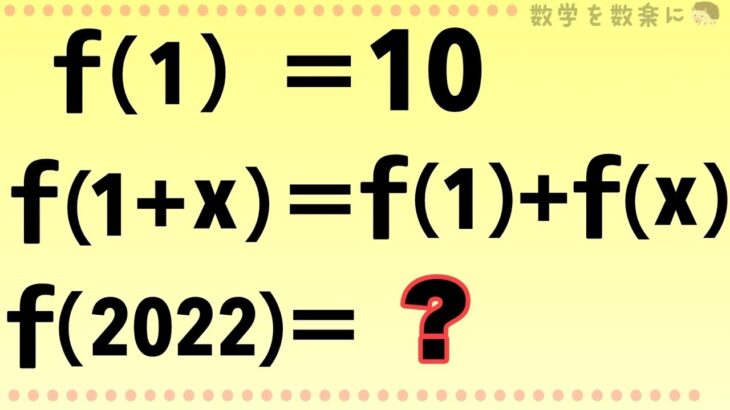
【視聴数 54560】
【チャンネル名 数学を数楽に】
【タグ 動画,ビデオ,共有,カメラ付き携帯電話,動画機能付き携帯電話,無料,アップロード,チャンネル,コミュニティ,YouTube,ユーチューブ】
「これするだけでおこずかい7000円ゲット!?」中学生でもスマホがあればできる期間限定キャンペーンを利用して7000円分ポイントをゲットする方法がこちらw
【また爆益キター!!】TikTokキャンペーンを利用して簡単に3200円貰う方法がこちらw【期間限定】
数学を数楽にする高校入試問題81
https://amzn.to/3l91w2K
オンライン個別指導をしています。
https://sites.google.com/view/kawabatateppei
数学Tシャツ販売中
https://suzuri.jp/suugaku
6:05
x∈Nのときのみでは
関数の形をしているように見えますが
実質、等差数列の漸化式ですね。
はじめて自分でわかった!
うれしい!
何か微分したり色々やってみたけど良く分からなくて、結局一時間位で単純に10倍したものに気づいた😂
wenchebatch mobitz must not comment
4, 46
次回の問題
答えの1つは殿馬
高校数学ですね。
確か高3数学の範囲だったような…
考え方は単純だけどややこしや…
n=4、46
n=4,46
帰納法で証明が必要でしょうか?
なるほど、これが漸化式ってやつか。はなおが敗北した領域までもう一歩だな。
線形なことが示されてるからね
f(0)=0
f(1)=10
f(2)=20
f(3)=30
f(4)=40
以上より、f(x)=10xと推測できるので、証明してみる。
取り敢えず今回はxは正の整数に限るものとする。というか分かりやすくnとする。
f(n)=10n…(*)を証明する。
(i)n=1のとき、
f(1)=10より(*)は成り立つ。
(ii)n=kのとき、(*)が成り立つと仮定すると、n=k+1のとき、f(k+1)=10(k+1)となることを証明すればよい。
f(k+1)
=f(1)+f(k)
=10+10k
=10(k+1)
よって(*)は成り立つ。
(i),(ii)より、f(n)=10nである。
2022は正の整数なので当然↑が使える。
f(2022)=20220
京大のやつに似てるわ
function!
数列いいですね。基礎解析ではこのあと微積分の基本にいくんでした。記号が多くなって数式がかっこよくなるんですよ。そのあと微分積分で極限使って高度な解析する。楽しい分野ですね。
同じ方法で解きました。
確かに川端先生の動画ではf(x)を扱った問題って初めて見ました。
xに1から順々に1ずつ増やして何個か代入していけばパターンが見えてきますね。
f(x+1)-f(x)=f(1)=10て変形してバサバサやるかと期待してましたら、ちょっと違った。
SPIでこんなの出てくるよね
xが整数以外の場合のf(x)は一切わからないので、これだけでf(x)=10xと言うのは乱暴すぎですよね。
次のやつ4と46かな
f(x)とは何か。
授業では3分で話されてその後すぐに当たり前のように使われるので、数学が苦手な人は混乱します(今までy=だったじゃん?!と)。
更に、f(x)もy=axも同じようなものだし好きな方を使えばいいよと言う人もいるから大混乱。
混乱している中でドンドン授業は進みます。
このように丁寧に教えてくれるのはありがたいと思います。
いつもと違う系統の問題でしたが、頭の体操になって楽しかったです
代数・幾何のベクトル、懐かしいなぁ。数列やったなぁ⁉︎
典型的な線形性のある関数ですね。
パッと見て、haskellのソースコードかと思いました。
f(x)=10x f(2022)=20220
大学ではこの関数を加法的関数といいます。稠密性を証明できるのですべての実数xに対してf(x)=axとなります。
一橋に似たようなのあったな
「P(0)=1,P(x+1)-P(x)=2xを満たす整式P(x)を求めよ」ってやつ
これは偶然なんですけどf(1)=10をf×1=10のように見るとfの一次方程式になるのでこれを解くとf=10となり、求める値はf(2022) だからfを2022倍するとf(2022)=20220となって動画と同じ値が得られました。
6:05 fの連続性を仮定すれば、ですね
発展 f(1+x)=f(f(x)+1)となる関数f(x)を全て求めよ
数列的表現
この問題とはまったく関係無いですが、昔関数は「函数」と書いて「かんすう」と読んだそうです。
ある数xをブラックボックスの中に入れてガチャガチャしたら、それに対応する数yが出てくるイメージなんでしょうか。
f(x+1)=f(1)+f(x)に対して、xにx-1,x-2,…,0を代入してx個の式を作ってすべての辺辺を足すと、ザクザク相殺されてf(x)=xf(1)+f(0)になる。元の式にx=0を代入するとf(0)=0とわかるのでf(x)=10x。
f(x)とは何か?という基本的な考え、ちゃんとわかってなくて数3で合成関数の微積が出てきたときに詰んで、数1からやり直した記憶があります
大学の受験でも問われる事もある問題で
f(x)の正しい扱い方を理解するのに
とても良いと思いました
敢えてf(x)で表現してますが
要するに数Bの漸化式ですね
a1=10
an+1=a1+an
a2022を求めよ
という感じの漸化式となります
公差が10の等差数列なので
an=a1+a(n-1)d (a1:初項 d:公差)
an=10+(n-1)*10
an=10n
a2022=20220
あと今回ではf(x)=10xで
これが成り立つ前提で
話が進んでいますが
xがどういった条件で成り立つのかを
議論をする必要があります
今回はxが自然数で成り立ちますが
もしかしたら10xが
成り立たないかもしれませんので
気をつけましょう
公差が10の等差数列で初項が10だから迷う要素全くなし。計算ドリルレベル。👎😲
受験中にうっかり、ひっかけ問題かなと思って取り組むと、ドツボにはまりそうな問題だと思いました。
これ昔エクセルやってから理解したわ
f(x)=とか数学で使われる様になって最初凄い違和感あったなぁ
線☆型☆写☆像☆
これ大学入試なのか
答えはすぐ出てくるけどちゃんと論述できる自信がない
f(1)=1 に見えて環の準同型写像の問題かと思った
f(x)=10[x]
([ ]はガウス記号)
とかも条件を満たす関数の一つですね。
数列の漸化式として解くのが一番速い!
皆f(2)とかf(3)とかからやってくのか。
普通にf(1+2021)を二つ目の式に倣って式変形して、降下させてって答え出したわ
1変化した時にf(x)+f(1)のように分解できるならf(1)+f(2021)も出来るのではないかといことで一瞬で20220は出ました!
f(x)は分からないけれどxが整数値の時は帰納的に求まるって問題
乗法に関して定義されてないから、関数がベクトル空間であるとは言えないんだよなー